Paul Tee's Site

Recall the goal of the maximum subarray problem is given an integer array $A$ , find a subarray $S$ such that the sum of the entries $S$ is maximized among all subarrays of $A$ . Kandae's solution is, roughly speaking, greedily maximize wrt no non-positive prefixes. We provide a graphical interpretation of this explanation.

${}$

We interpret $A$ as narrating the movement along a path starting at an arbitrary initial position. From this, we graph out the current position. In other words, we interpret a positive/negative integer $a\in A$ as moving right/left from our current position by $|a|$ units. Maximizing subarray sum is equivalent to maximizing the displacement along this path.

${}$

For example, suppose $A=[1,2,-4,7,-2,5,-10,5]$ . Assuming our initial position is at $0$ , then the plot associated to $A$ is given by the picture below.

${}$

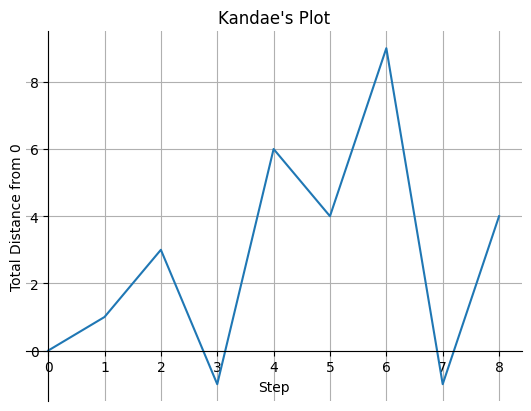
Plot associated to [1,2,-4,7,-2,5,-10,5].

${}$

Notice that there are two non-positive prefixes, namely the subarrays $[1,2,-4]$ and $[7,−2,5,−10]$ . In the plot, these would constitutes as "restarts", since they take down to or below the previous minimum. Between each "restart" we can just obviously employ a simple greedy scheme of keeping max displacement.

${}$

An alterantive interpretation is to interpret the above plot as the price action chart of a stock. Under this interpretation, we see that this problem becomes best time to buy and sell stock.